Primera Ley de Kepler
Copérnico y Galileo supusieron que las órbitas planetarias eran circulares, mientras que el Sol se ubicaba en el centro de dichas circunferencias concéntricas. Johannes Kepler (1571–1630), contemporáneo de Galileo, cuando revisaba personalmente las anotaciones de las posiciones de los astros efectuadas durante muchos años por su maestro, el astrónomo danés Tycho Brahe (1546–1601), notó que la órbita de Marte no era una circunferencia perfecta, sino que se parecía ligeramente a un óvalo. Se presentaban entonces dos posibilidades básicas: o bien había errores en los datos, o bien las órbitas no eran circulares. Kepler, que conocía cuán meticuloso y preciso era su maestro, luego de largo tiempo de revisión de los datos que éste había obtenido a simple vista (todavía no existía el telescopio, que fue inventado siete años después de la muerte de Tycho Brahe) se decidió por la segunda opción. Esto lo llevó a formular una hipótesis que se conoce como la Primera Ley de Kepler:
Las órbitas de los planetas son elípticas y el Sol se encuentra en uno de los focos de
dichas elipses.
El postulado de la circularidad de las órbitas de los planetas tenía una historia de unos 2000 años. El abandono de esta idea por parte de Kepler no fue una decisión tomada de un día para el otro, sino que le llevó mucho tiempo de dudas, hipótesis, cálculos y revisión de los datos observacionales de Brahe. Sin embargo, pasados algunos años, esta nueva hipótesis fue aceptada por la comunidad científica. Así, el Sol dejó de ocupar el punto central del sistema solar, de la misma manera que con Copérnico la Tierra había sido desplazada de dicho lugar. El hombre no se encontraba en el centro del universo. El Sol, expresión de la luz divina, tampoco.
La excentricidad de las órbitas
Se llama excentricidad, e, de una elipse a un número entre 0 y 1 que indica en qué grado esta figura difiere de una circunferencia. Si la excentricidad es cero, entonces la elipse coincide con la circunferencia y cuanto más cercano a 1 es el valor, entonces más alargada es la elipse.
Las órbitas planetarias son muy poco excéntricas. Si bien son elipses, son aproximadamente circulares. La excesiva forma elíptica de las órbitas planetarias en las ilustraciones que se observan habitualmente en libros y revistas pretenden hacer hincapié precisamente en las formas elípticas y no en qué grado lo son.
La excentricidad de la órbita terrestre es menor que 0,02, lo cual expresa que su forma es casi indistinguible de una circunferencia. La excentricidad de la órbita de Marte es casi 5 veces mayor que la de la Tierra, siendo la diferencia entre el diámetro mayor y el diámetro menor de 0,005. En cambio, la excentricidad de la órbita del cometa Halley es 0,97.
Además de su famosa primera ley, Kepler formuló otras dos, menos conocidas en general pero no por ello menos importantes.
Segunda Ley de Kepler
La Segunda Ley de Kepler, presentada conjuntamente con la primera en su obra Nueva Astronomía (1609), afirma que:
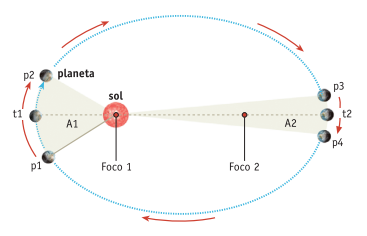
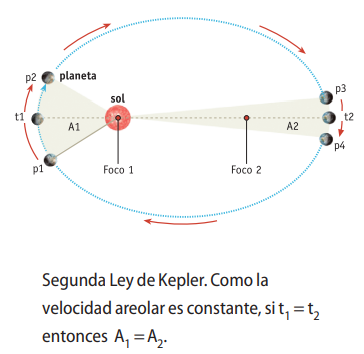
La rapidez de un planeta es tal que una línea imaginaria trazada desde el centro del Sol al centro del planeta barre áreas iguales en iguales intervalos de tiempo.
Si se llama rapidez areolar media al cociente entre el área que barre el segmento que une al centro del planeta con el centro del Sol y el tiempo transcurrido, entonces la Segunda Ley puede expresarse diciendo que la rapidez areolar de un planeta en su traslación alrededor del Sol es constante. Dado que las órbitas son elípticas, los planetas deben variar su rapidez para barrer iguales áreas en el mismo tiempo. La rapidez de traslación de cada planeta es mayor cuando se encuentra más cercano al Sol, y es menor cuando se halla más lejos de éste. El punto de mayor rapidez es el de mayor aproximación al Sol y se denomina perihelio, mientras que el de menor rapidez, el de mayor distancia radial al Sol, se llama afelio.
Tercera Ley de Kepler
La Tercera Ley describe la relación entre la distancia media de un planeta al Sol y su período de traslación (tiempo que tarda en realizar un giro completo alrededor del Sol) y afirma que:
Los cuadrados de los períodos de los planetas son proporcionales a los cubos de sus distancias medias al Sol.
Esta ley se puede enunciar diciendo que el cuadrado del período dividido por el cubo de la distancia media al Sol es constante para todos los planetas, es decir el cociente da por resultado el mismo valor para todos ellos. Por lo tanto:
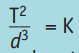
donde T es el período de traslación de un planeta alrededor del Sol, d es la distancia media del centro del planeta al centro del Sol y K es una constante.
Como este cociente da lo mismo para cualquier planeta, para calcular la constante K, se puede tomar el planeta Tierra. En este caso, si se considera como unidad de tiempo el año terrestre, y como unidad de distancia la unidad astronómica (UA) que es la distancia media entre el Sol y la Tierra, entonces se obtiene que:
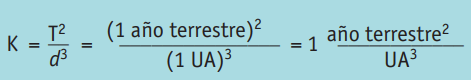
La unidad astronómica (UA) es la distancia media de la Tierra al Sol, que equivale aproximadamente a 150 millones de kilómetros.
Es decir:
1 UA = 150 000 000 km
Esta es una unidad de longitud utilizada en Astronomía para trabajar con valores de distancias muy grandes, del orden de las distancias interplanetarias
De esta manera se obtiene que el valor de K es igual a la unidad. Expresando los períodos orbitales en años terrestres, y la distancia orbital media en unidades astronómicas, el valor de la constante será siempre igual a 1 independientemente del planeta del que se trate. Así, a partir del período orbital de un planeta es posible calcular su distancia media al Sol.
Aplicaciones de la Tercera Ley de Kepler
Si se sabe que Kepler estimó el período de Marte ( TM) en 684 días terrestres, determinen la distancia media de Marte al Sol ( dM) tomando la Tierra como referencia.
Dado que el período de Marte es 684 días terrestres, su equivalente en años terrestres es:

de donde dM = 1,52 UA
Es decir, que la órbita media de Marte se encuentra 1,52 veces más alejada del Sol que la de la Tierra.
Como además 1 UA equivale a unos 1,5.10^11 m, entonces multiplicando esta cifra por 1,52 se obtiene la distancia media entre Marte y el Sol, o sea 2,28.10^11 m.
Las estaciones del año
En general, todo ser humano se hace representaciones del mundo a partir de la propia experiencia. Sin embargo, esas explicaciones y representaciones no necesariamente se corresponden con los hechos.
Dado que la órbita terrestre es elíptica, es común considerar que las estaciones del año se deben a la cercanía o a la lejanía de la Tierra con respecto al Sol. Desde este punto de vista no se tiene presente que cuando en el hemisferio Sur es verano, en el hemisferio Norte es invierno. Si se supone que la Tierra se encuentra en su punto de mayor acercamiento al Sol, no es cierto que en toda ella sea verano, ya que al mismo tiempo uno de los hemisferios se encuentra en invierno, que es la estación opuesta. Ante esta contradicción, se hace necesario presentar una nueva hipótesis.
El eje de rotación terrestre tiene una inclinación de unos 23,5º con respecto al plano de su órbita. Además, este eje mantiene su dirección prácticamente invariante a lo largo de toda la trayectoria planetaria. Esta inclinación es justamente la responsable de las estaciones del año, pues proporciona diferentes cantidades de radiación solar a los dos hemisferios.
En la época del año en la que el hemisferio Sur recibe mayor cantidad de radiación que el hemisferio Norte, entonces es verano para el primero e invierno para el segundo. Cuando, contrariamente, el que recibe mayor radiación solar es el hemisferio Norte, allí es verano

Actividades
- Calculen la distancia media de Júpiter al Sol sabiendo que el período de traslación alrededor del Sol es de 11,86 años terrestres.
- Calculen el período de traslación de Mercurio alrededor del Sol sabiendo que la distancia media entre ambos es de 57,91 millones de kilómetros.
- Ícaro es un asteroide que realiza un giro alrededor del Sol en 410 días. Calculen su distancia media al Sol.