Sir Isaac Newton fue uno de los físicos más importantes de la historia. Uno de los períodos más fructíferos de su producción fue entre los años 1665 y 1666 cuando se encontraba en su casa natal, escapando de una peste que azotaba Cambridge. Según cuenta la leyenda, mientras estaba sentado en su jardín, la caída de una manzana lo llevó a reflexionar y preguntarse si la fuerza que atraía la manzana hacia el suelo sería la misma que causaba que la Luna efectuase una órbita alrededor de la Tierra.
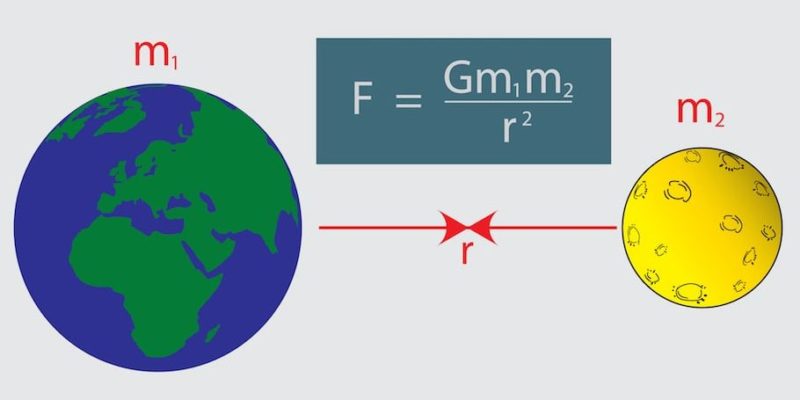
Luego de realizar sus cálculos y comparar los resultados con los datos observacionales, Newton comprendió que dos objetos cualesquiera se atraen entre sí, simplemente por el hecho de poseer masa. El valor de esta fuerza de atracción, llamada fuerza gravitatoria, depende de la masa de los objetos y de las distancias que separan sus centros. Además, por ser una fuerza que proviene de una interacción entre dichas masas, actúa en la dirección que une los centros de los dos cuerpos, es decir que es una fuerza central.
Si se consideran dos cuerpos de masas m1 y m2, separadas una distancia d, la ley de gravitación, formulada por Newton, establece que:
La intensidad de la fuerza de atracción gravitacional entre dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que separa sus centros.
Newton propuso que la Ley de Gravitación Universal es válida para todos los cuerpos del Universo; y se expresa en forma matemática mediante la ecuación:
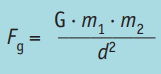
donde Fg es la fuerza gravitacional, G = 6,67 · 10–11 N · m2/ kg2 es la constante de gravitación universal; m1 y m2 son las masas de los cuerpos y d es la distancia que separa los centros de ambos.
La constante de gravitación universal G = 0,0000000000667 N · m²/kg² indica que dos cuerpos de 1 kg cada uno separados una distancia de 1 m, experimentan una fuerza gravitacional de 0,0000000000667 N, es decir, muy débil. Este tipo de fuerza solo se nota cuando uno o ambos cuerpos tienen mucha masa
Directamente proporcional al producto de las masas
Si se mantiene constante la distancia entre los dos cuerpos, cuanto mayor es el producto de las masas, mayor será también la fuerza gravitatoria que las atrae mutuamente. Por ejemplo, la fuerza gravitatoria entre la Tierra y un camión es mayor que entre la Tierra y una pelota.
Si se sustituye a los cuerpos por otros de mayor masa, entonces la fuerza entre ellos también es mayor. Si se los sustituye por otros de menor masa, la fuerza también es menor. En cambio, si una masa es reemplazada por una mayor mientras que la otra se sustituye por una menor, debe evaluarse necesariamente el producto entre ellas. Si este producto aumenta, entonces la fuerza será mayor, incluso si una de las masas es menor. En todos los casos, la fuerza aumenta o disminuye proporcionalmente al producto de las dos masas.
Inversamente proporcional al cuadrado de la distancia
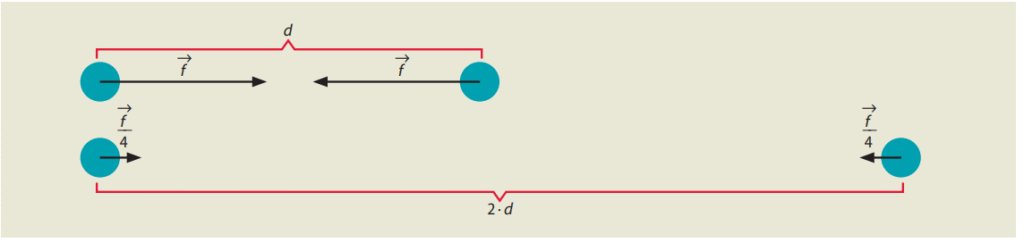
Si se duplica la distancia entre los centros de dos cuerpos, la fuerza se reduce 4 veces.
Si se mantienen constantes las masas de los cuerpos, cuanto mayor sea la distancia entre sus centros, menor será la fuerza gravitatoria entre ellos. Si la distancia se duplica, entonces la intensidad de la fuerza se reducirá a la cuarta parte. Si la distancia se triplica, esta se reduce a la novena parte, y así sucesivamente.
El valor de la fuerza gravitatoria entre el Sol y la Tierra a lo largo de su movimiento de traslación no es constante. Esta fuerza alcanza su valor máximo en el perihelio y su valor mínimo en el afelio.
Aclaraciones acerca de la Ley del Inverso del Cuadrado
Al analizar la interacción entre el planeta Tierra y una manzana a un metro de altura sobre su superficie, ¿se reducirá el valor de la fuerza gravitatoria a la cuarta parte si la manzana se eleva hasta los dos metros de altura? La fuerza gravitatoria no se reduce a la cuarta parte, dado que siempre se debe tener en cuenta que las distancias están medidas entre los centros de los cuerpos y no desde sus superficies.
Como el radio terrestre es de aproximadamente unos 6400 km, si un objeto que está a un metro de altura sobre la superficie se eleva hasta los dos metros, entonces, la distancia entre el centro del planeta y el objeto varía de 6 400 001 m a 6 400 002 m. Para calcular el valor de la fuerza gravitatoria en cada caso hay que tomar en cuenta que la masa de la Tierra es de 5,97 · 10^24 kg.
Si un objeto de 1 kg está a una distancia de 6 400 001 m del centro de la Tierra, su fuerza gravitatoria será:
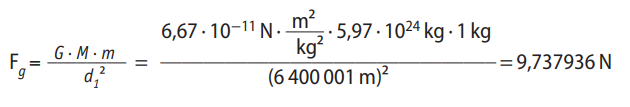
Si, en cambio, el objeto está a una distancia de 6 400 002 m del centro de la Tierra, entonces la fuerza gravitatoria se calcula como:
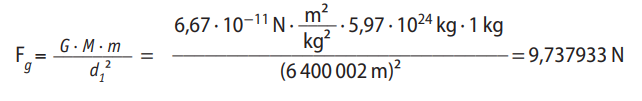
Se puede apreciar que la diferencia de valores surge recién en el sexto dígito decimal, lo que implica una diferencia de 0,000003 N. La diferencia entre estos valores es tan pequeña que el valor de la fuerza gravitatoria es prácticamente idéntico en ambos casos.
En general, un cuerpo próximo a la superficie terrestre es atraído por la Tierra con una fuerza que en muchos casos puede considerarse constante (varía de forma insignificante con la altura). Esta fuerza es precisamente el peso. Por ello, el peso de un objeto prácticamente no varía con la altura, a menos que ésta sea importante frente al radio terrestre.
Para calcular con precisión la fuerza gravitatoria que la Tierra ejerce sobre un objeto cualquiera de masa m a una altura h sobre su superficie, la ecuación para dicha fuerza puede escribirse de la siguiente manera:
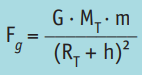
donde G es la constante de gravitación universal, M T es la masa de la Tierra, R T es el radio terrestre y m es la masa del objeto.
Fuerza gravitatoria en el interior de la Tierra
En el caso de cuerpos con gran radio, como la Tierra, la fuerza gravitatoria decrece a medida que aumenta la distancia desde su centro hasta el objeto, siempre y cuando se considere la masa total del planeta. Para que esto suceda, el objeto debe encontrarse a
cualquier altura sobre la superficie, pero no en el interior de dicho planeta.
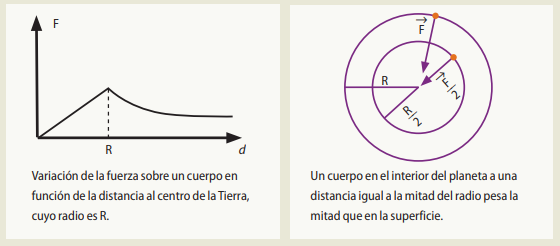
La fuerza gravitatoria en el interior de la Tierra no decrece a medida que aumenta la distancia desde su centro, sino que aumenta. Esto se debe a que al aumentar la distancia a un punto interior del planeta, también aumenta la masa que ejerce atracción hacia el centro, de manera tal que el resultado es un aumento lineal de la fuerza gravitatoria desde el centro del planeta hasta su superficie.
A una distancia del centro equivalente a la mitad del radio terrestre, el valor de la fuerza sobre un cuerpo es la mitad de lo que sería en la superficie.
En cambio, tomando como referencia la superficie terrestre, a medida que aumenta la profundidad, la fuerza gravitatoria sobre un cuerpo en su interior se reduce linealmente con la distancia.
La disminución de la fuerza gravitatoria de acuerdo con la Ley del Inverso del Cuadrado de la Distancia solo es válida para el caso en que se considera que dicho objeto se encuentra alejándose de la superficie terrestre en dirección al espacio exterior.
En síntesis, desde la superficie terrestre la fuerza gravitatoria sobre un cuerpo disminuye tanto al adentrarse en el planeta como al alejarse de él hacia el espacio exterior,
aunque siguiendo leyes diferentes en ambos casos.
Consecuencias de la Ley de Gravitación
La Ley de Gravitación Universal explica fenómenos tan distintos como la caída de los objetos, el movimiento de los planetas, de los satélites como la Luna, o el fenómeno de las mareas. Es importante destacar que Newton no descubrió la gravedad sino su validez universal. Es decir, descubrió que la fuerza de atracción gravitatoria existe siempre entre cuerpos por el simple hecho de poseer masa, sean éstos con mucha masa y distantes como estrellas, e incluso galaxias, o poco masivos y cercanos como pelotas o nueces.
La fuerza gravitatoria tiene, además, un alcance infinito y, si bien disminuye rápidamente a medida que los cuerpos se alejan el uno del otro, su valor nunca será exactamente cero, aunque se puedan despreciar sus efectos. Esto también implica que es imposible aislar absolutamente un cuerpo, ya que siempre está sometido a la influencia de la atracción gravitatoria del resto de partículas y cuerpos presentes en el universo, por más lejos que estos se encuentren.
Las consecuencias filosóficas y religiosas derivadas a partir de la Ley de la Gravitación Universal también han sido fundamentales para el pensamiento humano. A través de ella Newton logró establecer de un modo contundente que la división entre los mundos terrestre y celeste propuesta por Aristóteles era innecesaria. No hay leyes naturales diferentes para explicar lo que sucede en la Tierra y en el cielo. Las leyes que rigen los movimientos terrestres y celestes son las mismas, y con ello se unificó todo el universo y se puso fin al proceso de ruptura con la Física aristotélica que Galileo había comenzado con sus trabajos de Astronomía y Cinemática.
El movimiento de los planetas
Los planetas se trasladan alrededor del Sol bajo la acción central de la fuerza gravitatoria. Durante mucho tiempo se consideró erróneamente que sobre los planetas actuaba constantemente una fuerza en la dirección tangencial al movimiento, de manera que los empujaba a lo largo de su recorrido.
Valiéndose de sus Leyes del Movimiento y de la Gravitación Universal, Newton explicó el movimiento planetario. En ausencia de fuerzas externas, un planeta dotado de cierta velocidad tendería a seguir en una trayectoria rectilínea y a velocidad constante, de acuerdo con la ley de inercia. Sin embargo, el planeta describe una curva debido a la acción de la fuerza gravitatoria hacia el Sol, que lo desvía de su trayectoria rectilínea en cada uno de sus puntos. Como primera aproximación, puede decirse que a lo largo del desplazamiento elíptico del planeta, solo actúa la fuerza gravitatoria que lo atrae hacia el Sol, sin necesidad de otras fuerzas que lo impulsen hacia adelante.
Sin embargo, para un análisis más profundo, es necesario tener en cuenta las fuerzas gravitatorias que ejercen el resto de los planetas.
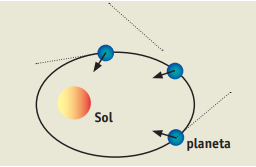
Este gráfico representa un planeta que está en órbita y en el cuál actúa solamente la
fuerza gravitatoria hacia el Sol.
(Podés descarga este material en formato PDF acá)